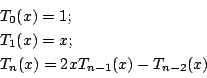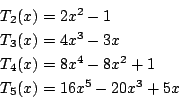周波数フィルターの基礎
begun: 2006/平成18 年9月28日
updated at: 平成19年2月7日
フィルターというのは一般的には瀘過器や篩(ふるい)のことで,ラテン語の
filtrum(瀘過用のフェルト.feltは同語源)に由来する.より本質的な定義では,
なにかの中から,ある条件に叶うものだけを抽出するための道具をフィルターと
云ふ.電気工学・電子工学そして信号数学・情報数学における周波数フィルター
は,様々な周波数から構成される信号の中から,ある特定の周波数成分だけを取
り出す装置のことである.
なお,フィルターは工学での正書法では「フィルタ」と記述する(カナ書きす
る外来語は語尾が長音で終わるものであっても「ー」を書かない.例外は日本
語にした時1に2音節以下のも
のは付ける.例:ルビー).そのため,本稿でもフィルタと記述する.
フィルタは方法論の違いから二種類に分けられる.一つはデータストリームを
フーリエ変換して,特定の周波数に対して演算を行い,逆フーリエ変換してデー
タストリームに復調するもの,もう一つは,フーリエ変換を経由せずに,直接
演算を行うものである.後者をコンボルーションと呼ぶ.
また,データストリームが連続量か離散量かによって,フィルタはアナログフィ
ルタとデジタルフィルタに区別できる.
- 通過(帯)域(passband)
- フィルタで抽出される信号の周波数帯域.フィ
ルタを通過する帯域.通過帯域の終わりの周波数を通過域端周波数(passband
edge frequency)と呼ぶ.
- 減衰(帯)域(stopband)
- フィルタで除去される信号の周波数帯域.フィ
ルタで減衰させられる帯域.
- 阻止(帯)域(stopband)
- 減衰域に同じ.減衰と云ふと「減って衰へたけ
ど多少はある」ようなニュアンスを含む可能性がある(減衰量/attenuation)の
で,通過率0%の場合は,通さないとふ意味の「阻止」を使うほうが望ましい.
阻止域の終わりと阻止域端周波数(stopband edge frequency)と呼ぶ.
- 遷移域(transition band)
- 通過域と減衰域の間の周波数帯域を遷移域
と云ふ.遷移域では応答特性が0以上1未満のでなければいけない.また,
応答特性がなだからに0から1に移行することが望ましい.
- 遮断周波数(cutoff frequency)
- 通過帯域と減衰帯域の境界.境界には,
常に境界問題(どこを境界にするか)がつきまとう.特に理想フィルタと違い,
実際のフィルタでは通過域と減衰域との境界がはっきりしない.端周波数は,
それぞれの帯域の終わりと示しているのであって,間に遷移帯が挟在している.
一般的には,
遮断周波数は,
となる周波数を云う.ここでGは利得(ゲイン; gain)である.なぜ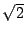 かという
と,タネがある.利得はしばしば電圧で示されるが,波動にとって重要なのはエ
ネルギである.単位時間あたりのエネルギーは電力である.電力は電圧の二乗に
比例するから,電力(エネルギ)が半分になる時,
電圧は
かという
と,タネがある.利得はしばしば電圧で示されるが,波動にとって重要なのはエ
ネルギである.単位時間あたりのエネルギーは電力である.電力は電圧の二乗に
比例するから,電力(エネルギ)が半分になる時,
電圧は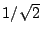 になる.故に
になる.故に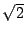 なのである.
たとえば,Butterworthフィルタような一次フィルタ(後述)の場合,
通過帯域から-3dB減衰した点(dBについて
は辻野(2006)を参照または自習されたし)で定義される.
なのである.
たとえば,Butterworthフィルタような一次フィルタ(後述)の場合,
通過帯域から-3dB減衰した点(dBについて
は辻野(2006)を参照または自習されたし)で定義される.
- 中心周波数(central frequency)
- Bandpassフィルタにおける通過域(ノッチフィルタの場合は減衰域)の中心の周波数.
今,上限の周波数を
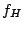 ,下限の周波数を
,下限の周波数を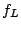 とすると,中心周波数
とすると,中心周波数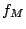 は
相乗平均(幾何平均)
は
相乗平均(幾何平均)
で与へられる.音楽や音波のように倍とか桁で取り扱う系つまり,対数でハ
ンドルする系では,平均と云へば幾何平均である.その理由は,
となるためである.
- 選択度(Q; selectivity)
- Bandpassフィルタにおける通過域(ノッチフィルタの場合は減
衰域)の幅
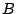 と中心周波数
と中心周波数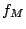 で与へられる数で,
で与へられる数で,
で定義される.
Qが大きいほど幅が狭いということであるから,通過域が狭くなりフィルタで抽
出される周波数成分が限定される(つまり選択度が強い).逆にQが狭いほど幅が
広い,ブロードな周波数成分を抽出するフィルタである.
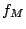 を掛けているのは,同じ幅の広さでも周波数によって,幅の広さのもつ意
味が異なるためである.
を掛けているのは,同じ幅の広さでも周波数によって,幅の広さのもつ意
味が異なるためである.
- 減衰特性(attenuation property)
- 減衰の性質.遷移域でのフィルタ函数の曲線の形状を指すことが多い.ただし,かふいふ曖昧な語はいろいろな使われ方をするので注意が必要である.
- 減衰度(attenuation)
- 減衰域での減衰度合い.減衰域ではまったく信号を遮断する必要
はなく,一律低減してもよい.
- 減衰傾度(attenuation factor, attenuation slope)
- 遷移域で利得が減衰する時の傾きを指す.フィルタ特性の傾き.
で定義できる.ここで 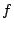 は周波数(frequency)である.
は周波数(frequency)である.
減衰傾度は dB/oct や dB/dec とふ単位で表わされる.
- dB/oct
- octはoctal(8進数)という意味はなく,オクターブ(octave)2の意
である.dB/octは,減衰傾度を,オクターブすなわち周
波数が倍になった時にどれだけ減衰しているかをdBで表わしたものである.
- dB/dec
- decはdecade(十でひとつのユニット)の意で,dB/decはdB/octと同様に定義されてい
る.すなわち,周波数が10倍になった時にどれだけ減衰しているかをdBで表わし
たものである.
dB/octとdB/decには対応関係があり,たとえば,Bandpassフィルタのような一次
フィルタの場合,20dB/decは6dB/octに等しい.
dB/decの考へ方は10を単位にしていることから,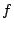 を
を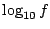 に変換して
ハンドルすることを意味している.一方,dB/octは倍(2)を単位にしていることから,
に変換して
ハンドルすることを意味している.一方,dB/octは倍(2)を単位にしていることから,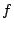 を
を
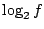 に変換してハンドルすることを意味している.両者の比をとってやると,
に変換してハンドルすることを意味している.両者の比をとってやると,
となる.したがって,dB/octをdB/decに変換するには,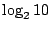 を掛けてや
ればよい.逆にdB/decをdB/octに変換するには,
を掛けてや
ればよい.逆にdB/decをdB/octに変換するには,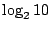 で除してやればよ
い.ちなみに,
で除してやればよ
い.ちなみに,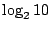 は約 3.321928である.
は約 3.321928である.
- 次数(order)
- 次数理想測定を近似するフィルタ函数の次数.次数が高
いほど理想に近い近似である.たとえばデジタルフィルタでは,フィルタは線
形差分方程式で表わされる.
たたし,x(n)はn番目の入力で,y(n)はn番目の出力であり,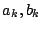 は係数
である.この式はフィルタ函数を
は係数
である.この式はフィルタ函数を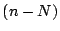 までの項の線形結合で表現するもの
である.この時,Nを無限に延長していけば,理想のフィルタ函数が得られる.
もっとも無限に線形結合を繰り返すことは,無限に手間がかかるので,ある程
度のところで打ち切る.大体において,4次が一般的な次数である.
までの項の線形結合で表現するもの
である.この時,Nを無限に延長していけば,理想のフィルタ函数が得られる.
もっとも無限に線形結合を繰り返すことは,無限に手間がかかるので,ある程
度のところで打ち切る.大体において,4次が一般的な次数である.
ある周波数を境として,それより低周波のものだけを通過させやうとするフィルタ.
対偶をとって,高域阻止フィルタ(highcut filter)と呼ばれることもある.
低域通過フィルタの逆.
Bandpass filterは低域通過フィルタ(lowpass filter)
と高域フィルタ(highpass filter)を組合せて,ある特定の周波数域を通過する
フィルタである.
Bandpassフィルタのlowpass とhighpassの組合せを逆にして,ある特定の周波
数域のみを阻止するフィルタ.阻止帯域が狭いものをノッチフィルタ
(notch filter)と呼ぶ.
Bandstopフィルタの通過帯域が著しく狭いもの.用途は,たとえば,信号帯域(見たい
情報が含まれている帯域)が10-80Hzの時に,観測器の故障で,ADの60Hzノイ
ズが載ってしまった場合に,60Hz(58-62?)のみを阻止するために用いる.
| Butterworth |
通過域がフラットになる. |
| Bessel |
過渡応答(立ち上がり/立ち下がり)が滑らか. |
| Tschebyscheffl(Chebyshevとも翻字される) |
遮断周波数の減衰傾度が大きい(急激な減衰). |
| 連立Tschebyscheff |
更に減衰傾度を大きくできる. |
周波数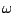 (正確には角速度/角周波数.真実の周波数は
(正確には角速度/角周波数.真実の周波数は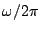 )に
対して次の式を満す振幅特性(周波数応答)をもつフィルタである(例として
Lowpass filterとして示す).
)に
対して次の式を満す振幅特性(周波数応答)をもつフィルタである(例として
Lowpass filterとして示す).
ここで,Nは次数, 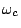 は遮断周波数である.これをButterworth特性という.振幅特性をみてわかることは,第一に,この函数は通過帯域では平坦になること,第二に,次数が高いほど減衰傾度が大きくなる(急激に減衰する)ことが予想される.
は遮断周波数である.これをButterworth特性という.振幅特性をみてわかることは,第一に,この函数は通過帯域では平坦になること,第二に,次数が高いほど減衰傾度が大きくなる(急激に減衰する)ことが予想される.
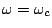 の時に振幅は
の時に振幅は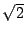 の減衰を示す.この時の減衰傾度は,
-6
の減衰を示す.この時の減衰傾度は,
-6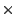 N dB/octである.
N dB/octである.
Tschebyscheffの多項式から求められるフィルタ.アナログ回路で多用される.
理想的なフィルタの応答特性は通過域で減衰0(100%通過)でかつ,遮断周波数
より阻止域では無限大の減衰(通過率0%)でなければいけない.しかし,アナ
ログフィルタでは抵抗やコンデンサ,コイルを用いるアナログ回路でフィルタ
を実装するため,有理関数の形をした伝達関数しか実装できない.したがって,
アナログ回路では,理想特性をいかに有理関数で近似するかということがフィ
ルタ設計の要である.有理関数の次数を大きくすると近似の具合は良くなる反
面,これを実現する回路は繁雑になっていく.無限次元の回路は思考できても,
実現不可能である.ものにはキリがあるので,必要な特性が得られる範囲で次
数はなるべく小さく必要がある.このような要請を満足するフィルタの設計方
法の一つとして,Tschebyscheffの多項式から求めるフィルタがある.
Tschebyscheffの多項式は,
の漸化式で示される一連の多項式である.たとえば,
と定義されている.
デジタルフィルタは,非巡回型と巡回型フィルタの二種類にわかれる.
非巡回型フィルタは,インパルス応答が有限長なので,Finit Impulse
Response(FIR)フィルタと呼ばれる.巡回型フィルタでは,出力が再度入力さ
れる再帰があるため,インパルス応答は無限長になる.故にInfinite Impulse
Responce(IR)フィルタと呼ばれている.
未稿.
平滑化処理,微分処理,デコン.自己相関函数.
中野ほか(1999)
- Camina, A.R.
- 1984,
Mathematics for seismic data.
Graham & Trotman,
London.
ISBN:0860105121/0860105768.
- 樋口龍雄・川又政征
- 2000,
MATLAB対応ディジタル信号処理.
昭晃堂.
227p.
ISBN:4785612010.
- 貴家仁志
- 1996,
よくわかるディジタル画像処理:フィルタ処理からDCT&ウェーブレットまで.
CQ出版
230p.
ISBN:4789836770.
- 南 茂夫・河田 聡
- 2002,
科学計測のためのテーダ処理入門.
CQ出版.
224p.
ISBN:4789836940.
- 中野宏毅・山本鎮男・吉田靖夫
- 1999,
ウェーブレットによる信号処理と画像処理.
共立出版.
174p.
ISBN:4320085493
- 小野浩司
- 1999,
シュミレーションで学ぶアナログ&ディジタルフィルタ入門.
日刊工業新聞.
268p.
ISBN:4526044814.
- 辻野 匠
- 2006,
デシベル(decibel)の簡単な解説.
http://staff.aist.go.jp/t-tsujino/doc/decibel/decibe.pdf (PDF版),
http://staff.aist.go.jp/t-tsujino/doc/decibel/decibel/decibe.html (HTML版)
- ...
語にした時1
- カナにするということは日本語にするということである.
チームとティームにしたところで英語になるわけではない.
- ... octはoctal(8進数)という意味はなく,オクターブ(octave)2
- オクターブは8音階(ドレミファソラシド)から構成されるので
oct (ラテン語で8の意.参考:オクトパス).1オクターブ上ると周波数は2倍に
ある.たとえば,ヘ音記号の側のラは440Hzであるが,1オクターブ上,ドレミファ
ソラシドレミファソラのラ(これをラ’と表記する)は880Hzである.
音楽関係者以外使っていないようなラであるが,ララララ’とすると,時報(ピッ,
ピッ,ピッ,ポーン)になる.
![]() を
を![]() に変換して
ハンドルすることを意味している.一方,dB/octは倍(2)を単位にしていることから,
に変換して
ハンドルすることを意味している.一方,dB/octは倍(2)を単位にしていることから,![]() を
を
![]() に変換してハンドルすることを意味している.両者の比をとってやると,
に変換してハンドルすることを意味している.両者の比をとってやると,
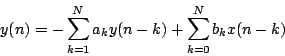
![]() は係数
である.この式はフィルタ函数を
は係数
である.この式はフィルタ函数を![]() までの項の線形結合で表現するもの
である.この時,Nを無限に延長していけば,理想のフィルタ函数が得られる.
もっとも無限に線形結合を繰り返すことは,無限に手間がかかるので,ある程
度のところで打ち切る.大体において,4次が一般的な次数である.
までの項の線形結合で表現するもの
である.この時,Nを無限に延長していけば,理想のフィルタ函数が得られる.
もっとも無限に線形結合を繰り返すことは,無限に手間がかかるので,ある程
度のところで打ち切る.大体において,4次が一般的な次数である.